Holonomic brain theory
Holonomic brain theory is a branch of neuroscience investigating the idea that consciousness is formed by quantum effects in or between brain cells. Holonomic refers to representations in a Hilbert phase space defined by both spectral and space-time coordinates.[1] Holonomic brain theory is opposed[citation needed] by traditional neuroscience, which investigates the brain's behavior by looking at patterns of neurons and the surrounding chemistry.
This specific theory of quantum consciousness was developed by neuroscientist Karl Pribram initially in collaboration with physicist David Bohm building on the initial theories of holograms originally formulated by Dennis Gabor. It describes human cognition by modeling the brain as a holographic storage network.[2][3] Pribram suggests these processes involve electric oscillations in the brain's fine-fibered dendritic webs, which are different from the more commonly known action potentials involving axons and synapses.[4][5][6] These oscillations are waves and create wave interference patterns in which memory is encoded naturally, and the wave function may be analyzed by a Fourier transform.[4][5][6][7][8]
Gabor, Pribram and others noted the similarities between these brain processes and the storage of information in a hologram, which can also be analyzed with a Fourier transform.[2][9] In a hologram, any part of the hologram with sufficient size contains the whole of the stored information. In this theory, a piece of a long-term memory is similarly distributed over a dendritic arbor so that each part of the dendritic network contains all the information stored over the entire network.[2][9][10] This model allows for important aspects of human consciousness, including the fast associative memory that allows for connections between different pieces of stored information and the non-locality of memory storage (a specific memory is not stored in a specific location, i.e. a certain cluster of neurons).[2][11][12]
Origins and development
[edit]In 1946 Dennis Gabor invented the hologram mathematically, describing a system where an image can be reconstructed through information that is stored throughout the hologram.[4] He demonstrated that the information pattern of a three-dimensional object can be encoded in a beam of light, which is more-or-less two-dimensional. Gabor also developed a mathematical model for demonstrating a holographic associative memory.[13] One of Gabor's colleagues, Pieter Jacobus Van Heerden, also developed a related holographic mathematical memory model in 1963.[14][15][16] This model contained the key aspect of non-locality, which became important years later when, in 1967, experiments by both Braitenberg and Kirschfield showed that exact localization of memory in the brain was false.[10]
Karl Pribram had worked with psychologist Karl Lashley on Lashley's engram experiments, which used lesions to determine the exact location of specific memories in primate brains.[2] Lashley made small lesions in the brains and found that these had little effect on memory. On the other hand, Pribram removed large areas of cortex, leading to multiple serious deficits in memory and cognitive function. Memories were not stored in a single neuron or exact location, but were spread over the entirety of a neural network. Lashley suggested that brain interference patterns could play a role in perception, but was unsure how such patterns might be generated in the brain or how they would lead to brain function.[17]
Several years later an article by neurophysiologist John Eccles described how a wave could be generated at the branching ends of pre-synaptic axons. Multiple of these waves could create interference patterns. Soon after, Emmett Leith was successful in storing visual images through the interference patterns of laser beams, inspired by Gabor's previous use of Fourier transformations to store information within a hologram.[18] After studying the work of Eccles and that of Leith,[17] Pribram put forward the hypothesis that memory might take the form of interference patterns that resemble laser-produced holograms.[19] In 1980, physicist David Bohm presented his ideas of holomovement and Implicate and explicate order.[20] Pribram became aware of Bohm's work in 1975[21] and realized that, since a hologram could store information within patterns of interference and then recreate that information when activated, it could serve as a strong metaphor for brain function.[17] Pribram was further encouraged in this line of speculation by the fact that neurophysiologists Russell and Karen DeValois[22] together established "the spatial frequency encoding displayed by cells of the visual cortex was best described as a Fourier transform of the input pattern."[23]
Theory overview
[edit]Hologram and holonomy
[edit]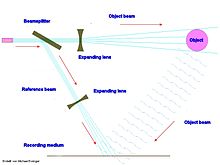
A main characteristic of a hologram is that every part of the stored information is distributed over the entire hologram.[3] Both processes of storage and retrieval are carried out in a way described by Fourier transformation equations.[24] As long as a part of the hologram is large enough to contain the interference pattern, that part can recreate the entirety of the stored image, but the image may have unwanted changes, called noise.[9]
An analogy to this is the broadcasting region of a radio antenna. In each smaller individual location within the entire area it is possible to access every channel, similar to how the entirety of the information of a hologram is contained within a part.[4] Another analogy of a hologram is the way sunlight illuminates objects in the visual field of an observer. It doesn't matter how narrow the beam of sunlight is. The beam always contains all the information of the object, and when conjugated by a lens of a camera or the eyeball, produces the same full three-dimensional image. The Fourier transform formula converts spatial forms to spatial wave frequencies and vice versa, as all objects are in essence vibratory structures. Different types of lenses, acting similarly to optic lenses, can alter the frequency nature of information that is transferred.
This non-locality of information storage within the hologram is crucial, because even if most parts are damaged, the entirety will be contained within even a single remaining part of sufficient size. Pribram and others noted the similarities between an optical hologram and memory storage in the human brain. According to the holonomic brain theory, memories are stored within certain general regions, but stored non-locally within those regions.[25] This allows the brain to maintain function and memory even when it is damaged.[3][24][26] It is only when there exist no parts big enough to contain the whole that the memory is lost.[4] This can also explain why some children retain normal intelligence when large portions of their brain—in some cases, half—are removed. It can also explain why memory is not lost when the brain is sliced in different cross-sections.[5]

Pribram proposed that neural holograms were formed by the diffraction patterns of oscillating electric waves within the cortex.[26] Representation occurs as a dynamical transformation in a distributed network of dendritic microprocesses.[27] It is important to note the difference between the idea of a holonomic brain and a holographic one. Pribram does not suggest that the brain functions as a single hologram. Rather, the waves within smaller neural networks create localized holograms within the larger workings of the brain.[6] This patch holography is called holonomy or windowed Fourier transformations.
A holographic model can also account for other features of memory that more traditional models cannot. The Hopfield memory model has an early memory saturation point before which memory retrieval drastically slows and becomes unreliable.[24] On the other hand, holographic memory models have much larger theoretical storage capacities. Holographic models can also demonstrate associative memory, store complex connections between different concepts, and resemble forgetting through "lossy storage".[13]
Synaptodendritic web
[edit]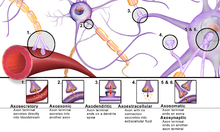
In classic brain theory the summation of electrical inputs to the dendrites and soma (cell body) of a neuron either inhibit the neuron or excite it and set off an action potential down the axon to where it synapses with the next neuron. However, this fails to account for different varieties of synapses beyond the traditional axodendritic (axon to dendrite). There is evidence for the existence of other kinds of synapses, including serial synapses and those between dendrites and soma and between different dendrites.[5] Many synaptic locations are functionally bipolar, meaning they can both send and receive impulses from each neuron, distributing input and output over the entire group of dendrites.[5]
Processes in this dendritic arbor, the network of teledendrons and dendrites, occur due to the oscillations of polarizations in the membrane of the fine-fibered dendrites, not due to the propagated nerve impulses associated with action potentials.[4] Pribram posits that the length of the delay of an input signal in the dendritic arbor before it travels down the axon is related to mental awareness.[5][28] The shorter the delay the more unconscious the action, while a longer delay indicates a longer period of awareness. A study by David Alkon showed that after unconscious Pavlovian conditioning there was a proportionally greater reduction in the volume of the dendritic arbor, akin to synaptic elimination when experience increases the automaticity of an action.[5] Pribram and others theorize that, while unconscious behavior is mediated by impulses through nerve circuits, conscious behavior arises from microprocesses in the dendritic arbor.[4]
At the same time, the dendritic network is extremely complex, able to receive 100,000 to 200,000 inputs in a single tree, due to the large amount of branching and the many dendritic spines protruding from the branches.[5] Furthermore, synaptic hyperpolarization and depolarization remains somewhat isolated due to the resistance from the narrow dendritic spine stalk, allowing a polarization to spread without much interruption to the other spines. This spread is further aided intracellularly by the microtubules and extracellularly by glial cells. These polarizations act as waves in the synaptodendritic network, and the existence of multiple waves at once gives rise to interference patterns.[5]
Deep and surface structure of memory
[edit]Pribram suggests that there are two layers of cortical processing: a surface structure of separated and localized neural circuits and a deep structure of the dendritic arborization that binds the surface structure together. The deep structure contains distributed memory, while the surface structure acts as the retrieval mechanism.[4] Binding occurs through the temporal synchronization of the oscillating polarizations in the synaptodendritic web. It had been thought that binding only occurred when there was no phase lead or lag present, but a study by Saul and Humphrey found that cells in the lateral geniculate nucleus do in fact produce these.[5] Here phase lead and lag act to enhance sensory discrimination, acting as a frame to capture important features.[5] These filters are also similar to the lenses necessary for holographic functioning.
Pribram notes that holographic memories show large capacities, parallel processing and content addressability for rapid recognition, associative storage for perceptual completion and for associative recall.[29][30] In systems endowed with memory storage, these interactions therefore lead to progressively more self-determination.[27]
Recent studies
[edit]While Pribram originally developed the holonomic brain theory as an analogy for certain brain processes, several papers (including some more recent ones by Pribram himself) have proposed that the similarity between hologram and certain brain functions is more than just metaphorical, but actually structural.[11][28][31] Others still maintain that the relationship is only analogical.[32] Several studies have shown that the same series of operations used in holographic memory models are performed in certain processes concerning temporal memory and optomotor responses. This indicates at least the possibility of the existence of neurological structures with certain holonomic properties.[10] Other studies have demonstrated the possibility that biophoton emission (biological electrical signals that are converted to weak electromagnetic waves in the visible range) may be a necessary condition for the electric activity in the brain to store holographic images.[11][31] These may play a role in cell communication and certain brain processes including sleep, but further studies are needed to strengthen current ones.[28] Other studies have shown the correlation between more advanced cognitive function and homeothermy. Taking holographic brain models into account, this temperature regulation would reduce distortion of the signal waves, an important condition for holographic systems.[11] See: Computation approach in terms of holographic codes and processing.[33]
Criticism and alternative models
[edit]Pribram's holonomic model of brain function did not receive widespread attention at the time, but other quantum models have been developed since, including brain dynamics by Jibu & Yasue and Vitiello's dissipative quantum brain dynamics. Though not directly related to the holonomic model, they continue to move beyond approaches based solely in classic brain theory.[3][11]
Correlograph
[edit]In 1969 scientists D. Wilshaw, O. P. Buneman and H. Longuet-Higgins proposed an alternative, non-holographic model that fulfilled many of the same requirements as Gabor's original holographic model. The Gabor model did not explain how the brain could use Fourier analysis on incoming signals or how it would deal with the low signal-noise ratio in reconstructed memories. Longuet-Higgin's correlograph model built on the idea that any system could perform the same functions as a Fourier holograph if it could correlate pairs of patterns. It uses minute pinholes that do not produce diffraction patterns to create a similar reconstruction as that in Fourier holography.[3] Like a hologram, a discrete correlograph can recognize displaced patterns and store information in a parallel and non-local way so it usually will not be destroyed by localized damage.[34] They then expanded the model beyond the correlograph to an associative net where the points become parallel lines arranged in a grid. Horizontal lines represent axons of input neurons while vertical lines represent output neurons. Each intersection represents a modifiable synapse. Though this cannot recognize displaced patterns, it has a greater potential storage capacity. This was not necessarily meant to show how the brain is organized, but instead to show the possibility of improving on Gabor's original model.[34] One property of the associative net that makes it attractive as a neural model is that good retrieval can be obtained even when some of the storage elements are damaged or when some of the components of the address are incorrect.[35] P. Van Heerden countered this model by demonstrating mathematically that the signal-noise ratio of a hologram could reach 50% of ideal. He also used a model with a 2D neural hologram network for fast searching imposed upon a 3D network for large storage capacity. A key quality of this model was its flexibility to change the orientation and fix distortions of stored information, which is important for our ability to recognize an object as the same entity from different angles and positions, something the correlograph and association network models lack.[16]
See also
[edit]- Gestalt psychology – Theory of perception
- Orchestrated objective reduction – Theory of a quantum origin of consciousness
- Quantum cognition – Application of quantum theory mathematics to cognitive phenomena
- Quantum mysticism – Pseudoscience purporting to build on the principles of quantum mechanics
- Self-organizing map – Machine learning technique useful for dimensionality reduction
- Sparse distributed memory – Mathematical model of memory
- Visual perception – Ability to interpret the surrounding environment using light in the visible spectrum
References
[edit]- ^ Pribram, Karl (1991). Brain and Perception: Holonomy and Structure in Figural Processing. Lawrence Erlbaum Associates, Inc. ISBN 0-89859-995-4.
- ^ a b c d e Forsdyke D. R. (2009). "Samuel Butler and human long term memory: Is the cupboard bare?". Journal of Theoretical Biology. 258 (1): 156–164. Bibcode:2009JThBi.258..156F. doi:10.1016/j.jtbi.2009.01.028. PMID 19490862.
- ^ a b c d e Andrew A. M. (1997). "The decade of the brain - further thoughts". Kybernetes. 26 (3): 255–264. doi:10.1108/03684929710163155.
- ^ a b c d e f g h Pribram K. H., Meade S. D. (1999). "Conscious awareness: Processing in the synaptodendritic web". New Ideas in Psychology. 17 (3): 205–214. doi:10.1016/S0732-118X(99)00024-0.
- ^ a b c d e f g h i j Pribram K. H. (1999). "Quantum holography: Is it relevant to brain function?". Information Sciences. 115 (1–4): 97–102. doi:10.1016/S0020-0255(98)10082-8.
- ^ a b c Vandervert L. R. (1995). "Chaos theory and the evolution of consciousness and mind: A thermodynamic-holographic resolution to the mind-body problem". New Ideas in Psychology. 13 (2): 107–127. doi:10.1016/0732-118X(94)00047-7.
- ^ Berger D.H., Pribram K.H. (1992). "The Relationship between the Gabor elementary function and a stochastic model of the inter-spike interval distribution in the responses of the visual cortex neurons". Biological Cybernetics. 67 (2): 191–194. doi:10.1007/bf00201026. PMID 1320946. S2CID 11123748.
- ^ Pribram K.H. (2004). "Consciousness Reassessed". Mind and Matter. 2: 7–35.
- ^ a b c Gabor D (1972). "Holography, 1948–1971". Science. 177 (4046): 299–313. Bibcode:1972Sci...177..299G. doi:10.1126/science.177.4046.299. PMID 4556285.
- ^ a b c Borsellino A., Poggio T. (1972). "Holographic aspects of temporal memory and optomotor responses". Kybernetik. 10 (1): 58–60. doi:10.1007/bf00288785. PMID 4338085. S2CID 10084612.
- ^ a b c d e Bókkon István (2005). "Dreams and neuroholography: An interdisciplinary interpretation of development of homeotherm state in evolution". Sleep and Hypnosis. 7 (2): 47–62.
- ^ Gabor D (1968). "Holographic Model of Temporal Recall". Nature. 217 (5128): 584. Bibcode:1968Natur.217..584G. doi:10.1038/217584a0. PMID 5641120. S2CID 4147927.
- ^ a b Kelly M. A.; Blostein D.; Mewhort D. J. K. (2013). "Encoding structure in holographic reduced representations". Canadian Journal of Experimental Psychology. 67 (2): 79–93. doi:10.1037/a0030301. PMID 23205508.
- ^ Van Heerden P. J. (1963). "A New Optical Method of Storing and Retrieving Information". Applied Optics. 2 (4): 387–392. Bibcode:1963ApOpt...2..387V. doi:10.1364/AO.2.000387.
- ^ Van Heerden P. J. (1963). "Theory of Optical Information Storage in Solids". Applied Optics. 2 (4): 393–400. Bibcode:1963ApOpt...2..393V. doi:10.1364/AO.2.000393.
- ^ a b Van Heerden P. J. (1970). "Models for the brain". Nature. 225 (5228): 177–178. Bibcode:1970Natur.225..177V. doi:10.1038/225177a0. PMID 5409963. S2CID 4224802.
- ^ a b c Pribram H.H. (2011). "Recollections". NeuroQuantology. 9 (3): 370–374. doi:10.14704/nq.2011.9.3.447.
- ^ Emmett N. Leith and Juris Upatnieks (1965). Photography by Laser. Scientific American Volume 212, Issue 6, June 1, 1965
- ^ K. Pribram (1969). The Neurophysiology of Remembering. American Volume 220, Issue 1, January 1, 1969
- ^ Bohm 1980.
- ^ The implicate brain by Karl H. Pribram, karlhpribram.com
- ^ DeValois and DeValois, 1980
- ^ Pribram 1986
- ^ a b c Srivastava V., Edwards S. F. (2004). "A mathematical model of capacious and efficient memory that survives trauma". Physica A: Statistical Mechanics and Its Applications. 333 (1–4): 465–477. Bibcode:2004PhyA..333..465S. doi:10.1016/j.physa.2003.10.008.
- ^ Longuet-Higgins H. C. (1968). "Holographic model of temporal recall [50]". Nature. 217 (5123): 104. Bibcode:1968Natur.217..104L. doi:10.1038/217104a0. PMID 5635629. S2CID 4281144.
- ^ a b Baev K.V. (2012). "Solution of the Problem of Central Pattern Generators and a New Concept of Brain Functions". Neurophysiology. 4 (5): 414–432. doi:10.1007/s11062-012-9313-x. S2CID 17264908.
- ^ a b Pribram, Karl (1991). Brain and Perception: Holonomy and Structure in Figural Processing. Laurence Erlbaum Associates, Inc. ISBN 0-89859-995-4.
- ^ a b c Persinger M.A., Lavallee C. (2012). "The Σn=n Concept and the Quantitative Support for the Cerebral-Holographic and Electromagnetic Configuration of Consciousness". Journal of Consciousness Studies. 19: 128–253.
- ^ Unterseher, Fred (1996). Holography Handbook: Making Holograms The Easy Way (Second ed.). Ross Books. pp. 354–359. ISBN 0-89496-016-4.
- ^ Pribram, Karl (1990). Prolegomenon for a Holonomic Brain Theory (PDF).
- ^ a b Shelli Joye (2020). The Electromagnetic Brain: EM Field Theories on the Nature of Consciousness. Inner Traditions, pp. 240-245. ISBN 978-0-9988785-6-0
- ^ Velmans M (2003). "Is the world in the brain, or the brain in the world?". Behavioral and Brain Sciences. 26 (4): 427–429. doi:10.1017/s0140525x03420098. S2CID 142563034.
- ^ Shlomi Dolev; Ariel, Hanemann (2014). "Holographic "Brain" Memory and Computation". Latin America Optics and Photonics: 16–21. doi:10.1364/LAOP.2014.LM2A.3. ISBN 978-1-55752-825-4.
- ^ a b Willshaw D. J.; Buneman O. P.; Longuet-Higgins H. C. (1969). "Non-holographic associative memory". Nature. 222 (5197): 960–962. Bibcode:1969Natur.222..960W. doi:10.1038/222960a0. PMID 5789326. S2CID 27768997.
- ^ Hinton, Geoffrey; Anderson, James (1989). Parallel Models Of Associative Memory. Lawrence Erlbaum Associates, Inc. pp. 115–116. ISBN 0-8058-0270-3.
Works cited
[edit]- Bohm, David (1980). Wholeness and the Implicate Order. London: Routledge. ISBN 0-7100-0971-2.
- Pribram, Karl (1986). "Holonomic Brain Theory In Imaging And Object Perception". Acta Psychologica. 63 (1–3): 175–210. doi:10.1016/0001-6918(86)90062-4. PMID 3591432.
- Pribram, Karl (1991). Brain and Perception: Holonomy and Structure in Figural Processing. Lawrence Erlbaum Associates.
Further reading
[edit]- Aerts, Diedrick; Czachor, Marek; Sozzo, Sandro (2011). Privman, V.; Ovchinnikov, V. (eds.). Quantum Interaction Approach in Cognition, Artificial Intelligence, and Robots. IARIA, Proceedings of the Fifth International Conference on Quantum, Nano and Micro Technologies. Brussels University Press. pp. 35–40. arXiv:1104.3345.
- Mishlove, Jeffrey (1998). "The Holographic Brain: Karl Pribram, Ph.D. interview". TWM.co.nz. Archived from the original on 2006-05-18. Retrieved 2012-05-18.
- Peruš, Mitja; Loo, Chu Kiong (2011). Biological And Quantum Computing For Human Vision: Holonomic Models And Applications. Medical Information Sciences Reference. ISBN 978-1615207855.
- Pribram, Karl (1993). Rethinking Neural Networks: Quantum Fields And Biological Data. Lawrence Erlbaum Associates and INNS Press.
- Pribram, Karl (2007). "Holonomic brain theory". Scholarpedia. 2 (5). Washington, DC: Georgetown University: 2735. Bibcode:2007SchpJ...2.2735P. doi:10.4249/scholarpedia.2735.
- Pribram, Karl (2013). The Form Within. Prospecta Press.
- Talbot, Michael (2011). The Holographic Universe. HarperCollins.
External links
[edit]- KarlPribram.com, hosts PDFs of Pribram's articles about HBT in English and Spanish
